CONTROL STRUCTURES USING POWER SERIES OF SINE
Do you wish to have more control in your life? Of course you do. Well that’s a story for a another day. However,did you know you can control a computer however you please. We shall do this using java control structures.
Imagine giving instructions to a child to bathe. You tell him/her to go into the bathroom and use water and soap. In the same way we give a computer instructions. You forgot to tell the child to remove his clothes before entering the bathroom.That’s exactly how a computer follows instructions.
Let’s look at the definition of sine particularly its Power series. Can it be defined?
Yes. The Power series of sine is defines as:
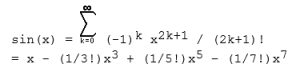
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – –
LIVE A LITTLE
What did the Science book say to the Math book?
You have problems men
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – –
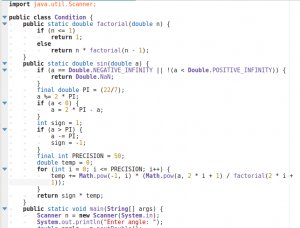
Let’s try computing this formular in java. Copy compile and run the following code:
Output:
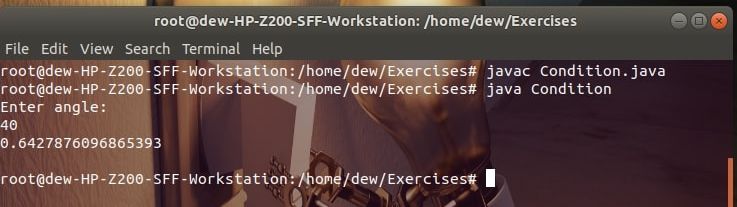
Explanation:
import java.util.Scanner;
public class Condition {
//method that does factorial of the denominator
public static double factorial(double n) {
// base case
if (n <= 1)
return 1;
else
return n * factorial(n – 1);
}
public static double sin(double a) {
if (a == Double.NEGATIVE_INFINITY || !(a < Double.POSITIVE_INFINITY)) {
return Double.NaN;
}
// If you can’t use Math.PI neither,
// you’ll have to create your own PI
final double PI = (22/7);
// Fix the domain for a…
// Sine is a periodic function with period = 2*PI
a %= 2 * PI;
// Any negative angle can be brought back
// to it’s equivalent positive angle
if (a < 0) {
a = 2 * PI – a;
}
// Also sine is an odd function…
// let’s take advantage of it.
int sign = 1;
if (a > PI) {
a -= PI;
sign = -1;
}
// Now a is in range [0, pi].
// Calculate sin(a)
// Set precision to fit your needs.
// Note that 171! > Double.MAX_VALUE, so
// don’t set PRECISION to anything greater
// than 84 unless you are sure your
// Factorial.factorial() can handle it
final int PRECISION = 50;
double temp = 0;
for (int i = 0; i <= PRECISION; i++) {
temp += Math.pow(-1, i) * (Math.pow(a, 2 * i + 1) / factorial(2 * i + 1));
}
return sign * temp;
}
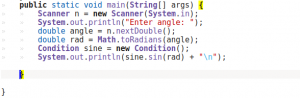
public static void main(String[] args) {
Scanner n = new Scanner(System.in);
System.out.print(“Enter angle: “);
double angle = n.nextDouble();
double rad = Math.toRadians(angle);
Condition sine = new Condition();
System.out.print(sine.sin(rad) + “\n”);
}
}
In order to achieve this presentation we used the following steps:
- Research on Power Series of Sine
- Understanding how the Power Series works
- Write a java code that solves the sine of any angle in degrees
- Compile, Debug and run the code
- Understanding the java code